Suslin's problem
In mathematics, Suslin's problem is a question about totally ordered sets posed by Mikhail Yakovlevich Suslin in a work published posthumously in 1920.[1] It has been shown to be independent of the standard axiomatic system of set theory known as ZFC: the statement can neither be proven nor disproven from those axioms.[2]
(Suslin is also sometimes written with the French transliteration as Souslin, from the Cyrillic Суслин.)
Contents |
Formulation
Given a non-empty totally ordered set R with the following four properties:
- R does not have a least nor a greatest element
- the order on R is dense (between any two elements there is another)
- the order on R is complete, in the sense that every non-empty bounded subset has a supremum and an infimum
- every collection of mutually disjoint non-empty open intervals in R is countable (this is the countable chain condition, ccc)
is R necessarily order-isomorphic to the real line R?
If the requirement for the countable chain condition is replaced with the requirement that R contains a countable dense subset (i.e., R is a separable space) then the answer is indeed yes: any such set R is necessarily isomorphic to R.
Implications
Any totally ordered set that is not isomorphic to R but satisfies (1) – (4) is known as a Suslin line. The existence of Suslin lines has been proven to be equivalent to the existence of Suslin trees. Suslin lines exist if the additional constructibility axiom V equals L is assumed.
The Suslin hypothesis says that there are no Suslin lines: that every countable-chain-condition dense complete linear order without endpoints is isomorphic to the real line. Equivalently, that every tree of height ω1 either has a branch of length ω1 or an antichain of cardinality 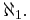
The generalized Suslin hypothesis says that for every infinite regular cardinal κ every tree of height κ either has a branch of length κ or an antichain of cardinality κ.
The Suslin hypothesis is independent of ZFC, and is independent of both the generalized continuum hypothesis and of the negation of the continuum hypothesis. However, Martin's axiom plus the negation of the Continuum Hypothesis implies the Suslin Hypothesis. It is not known whether the Generalized Suslin Hypothesis is consistent with the Generalized Continuum Hypothesis; however, since the combination implies the negation of the square principle at a singular strong limit cardinal—in fact, at all singular cardinals and all regular successor cardinals—it implies that the axiom of determinacy holds in L(R) and is believed to imply the existence of an inner model with a superstrong cardinal.
See also
Notes
- ^ Souslin, M. (1920). "Problème 3". Fundamenta Mathematicae 1: 223.
- ^ Solovay, R. M.; Tennenbaum, S. (1971). "Iterated Cohen extensions and Souslin's problem". Ann. Of Math. (2) (Annals of Mathematics) 94 (2): 201–245. doi:10.2307/1970860. JSTOR 1970860.
References
- Grishin, V.N. (2001), "Suslin hypothesis", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=S/s091460